先上图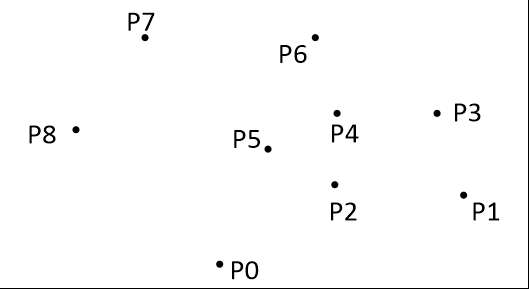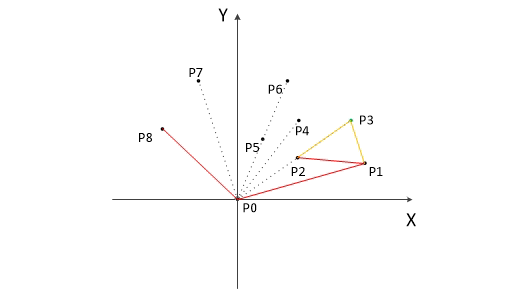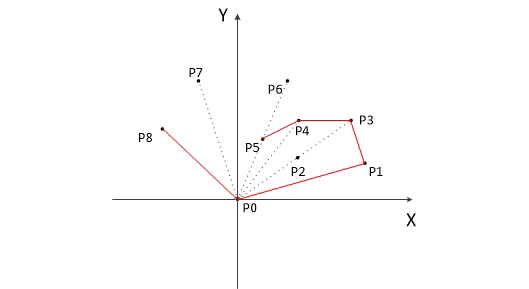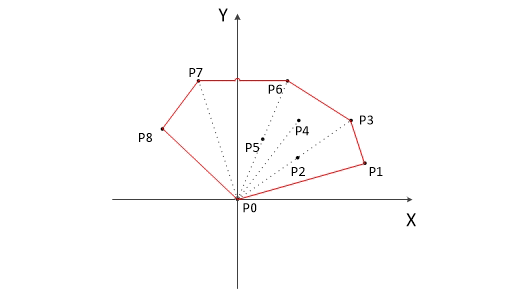

传统的Graham 扫描法
先排序，从左到右，从下到上
做两边，分别做上半部分和下半部分
用栈维护点，发现是凹的就退栈，但起点不能弹掉（WA了好久）
三点方向可用叉积判断
每一遍做完后栈中剩下的元素就是凸包的顶点

当年天真的我以为最短路图是有环的，然后翻了车

首先跑一遍$S$的最短路，记为$d$
用$dp\left [ x \right ][i]$记录点$x$，距离$\leq d_{x}+i$的方案数
转移方程如下

$$dp\left [ x \right ]\left [ i \right ]+=dp\left [ to \right ]\left [ i+d_{x}-d_{to}-val_{x-to} \right ]$$

这里的$x-to$是反图上的边
答案就是$dp\left [ T \right ]\left [ K \right ]$，初始化所有$dp\left [ S \right ]$为1

对于0 环，比较好的一种处理方式是记忆优化搜索
当处理$\left ( x,i \right )$时，再次搜到$\left ( x,i \right )$，则说明图中存在0 环

首先随便找一种长度的围栏，比如$p$
设$d\left [ r \right ]\equiv r\left ( mod \ p \right )$，且为最小的不能修建的长度
根据定义，$d\left [ r \right ]+t*p\left ( t \in \mathbb{N} \right )$均能修建，$d\left [ r \right ]+t*p\left ( t < 0\right )$均不能修建

求$d$的过程就是求最短路
首先$d\left [ 0 \right ]=0$，其次可用$d\left [ x \right ]+a_{i}$更新$d\left [ \left ( x+a_{i} \right ) mod \ p\right ]$
显然$p$越小，复杂度越低

当且仅当点$x$，存在一个子节点$dfn\left [ x \right ]\leq low\left [ x_{son}\right ]$，点$x$是割点
特别地，若$x$为搜索树的根，只要它有两个或以上子节点，它就是割点
因为是小于等于，所以在求割点时，不必考虑父节点和重边问题

当且仅当$edge\left ( u,v \right )$，存在$dfn\left [ u \right ]<low\left [ v \right ]$，它为桥
需要注意的是，当存在重边时，$dfn\left [ fa \right ]$可以用来更新$low\left [ x \right ]$

在记录$fa$的同时记录与$fa$的距离$d$
初始化$d$为0

先预处理出一行内所有可行方案，记为$s$，可以发现可行解并不多
再预处理出所有可行方案的炮兵数目，记为$w$
用$dp\left [ d\right ]\left [ i\right ]\left [ j \right ]$记录前$d$行，且上一行状态为$s_{j}$，上两行状态为$s_{i}$的最大炮兵数目

$$dp\left [ d \right ]\left [ j \right ]\left [ k \right ]=max\left \{ dp\left [ d-1 \right ]\left [ i \right ]\left [ j \right ]\right \}$$

转移时需要判断状态之间是否合法，炮兵是否均在平原

首先求一遍直径，记起点为$S$，终点为$T$
所有可行边均在直径上（废话）
考虑直径上某个点$x$，求出它不经过直径的能访问的最远距离，记为$d_{x}$
复杂度显然是$O\left(N\right)​$的

从$S$到$T$，依次遍历直径上所有点

• 若$d_{x}=D\left ( S,x \right )$，则$S$到$x$之间所有的边均不是必须经过的
• 若$d_{x}=D\left ( x,T \right )$，则$x$到$T$之间所有的边均不是必须经过的

需要注意的是，有些算法在遇到第二种情况时需要及时退出

$$\left\{\begin{matrix} x\equiv a_{1}\left ( mod \ m_{1} \right ) \\ x\equiv a_{2}\left ( mod \ m_{2} \right )\\ \cdots \\ x\equiv a_{n}\left ( mod \ m_{n} \right )\\ \end{matrix}\right.$$

不保证$m$两两互质

设已求出前$k$个方程的解，记为$x_{k}$
记$M_{k}=\prod _{i=1}^{k}m_{i}$
则$x_{k}+tM_{k}\left ( k \in\mathbb{Z} \right )$为前$k$个方程的通解

考虑第$k+1$个方程

$$x_{k}+tM_{k} \equiv a_{k+1} \left ( mod \ m_{k+1}\right )$$

用$exgcd$解出$t$
若无解则方程组无解
若有解则$x_{k+1}=x_{k}+tM_{k}$

其实$K$短路是有有理有据的做法的，但我不会啊

建立一个以$d$为关键字的优先队列
放入$\left ( S,0 \right )$，然后进行扩展
易证，当$\left ( x,d \right )$被第$K$次取出时，$d$为$S$到$x$的$K$短路

考虑用启发式优化来提高效率
到$T$的估计距离$f_{x}$可以为$x$到$T$的最短路
对于点$x$，$g_{x}=d_{now}+f_{x}$
优先队列以$g$为关键字

还可以继续优化

• 当取出其中某个点$K$次后，不需要将其再放入优先队列中
• 对于有距离要求的$K$短路，当取出元素的$d$大于给定值可直接退出