组合数学入门

写在前面

感觉组合数学是OI （高中数学）中比较难啃的一部分
还是得写点什么来总结一下
组合数$C,A$的有关性质这里就不赘述了，高中数学里有
水平不高，只能写一点个人的理解

小球与盒子

n 个球放入m 个盒子
这个应该是组合数学最经典的题目了

球相同，盒不相同

• 不允许空盒

  $$C_{n-1}^{m-1}$$

  经典的插板法，n 个小球有n-1 个空隙，插入m-1 块板，分成m 个集合

• 允许空盒

  $$C_{n+m-1}^{m-1}$$

  增加m 个球分给每个盒子，分好后从每个盒子中取出一个

球不相同，盒相同

• 不允许空盒

  $$S_{n}^{m}$$

  S 为第二类斯特林数

  递推公式

  $$S_{n}^{k}=k*S_{n-1}^{k}+S_{n-1}^{k-1}$$

  对于第n 个球
  它可以放入前面k 个盒子中，由于球不相同，可以产生k 种方案
  也可以自己放入一个新的盒子中
  易证其正确性

  边界条件

  $$S_{n}^{0}=0,S_{n}^{n}=1$$

• 允许空盒

  $$\sum _{i=0}^{n}S_{n}^{i}$$

  可以有$1-n$个空盒

球不相同，盒不相同

• 允许空盒

  $$m^{n}$$

  放入每个球时均有m 种方案

• 不允许空盒

  $$S_{n}^{m}*m!$$

  盒子不同，需要考虑顺序

球相同，盒相同

• 不允许空盒
  不会生成函数，只能用DP
  设$dp\left [ i \right ]\left [ j \right ]$为前i 个球，放入j 个盒子的方案数

  $$dp\left [ i \right ]\left [ j \right ]=dp\left [ i -1\right ]\left [ j-1 \right ]+dp\left [ i -j\right ]\left [ j \right ]$$
  • 若方案中有若干个盒子只有一个球，挑出其中一个盒子继续求解，方案数为$dp\left [ i -1\right ]\left [ j-1 \right ]$
  • 若方案中不存在某个盒子只有一个球，将每个盒子均取出一个球之后继续求解，方案数为$dp\left [ i -j\right ]\left [ j \right ]$

  答案为$dp\left [n \right ]\left [m \right ]$

  初始化$dp\left [0 \right ]\left [0 \right ]=1$

• 允许空盒

  $$dp\left [n+m \right ]\left [m \right ]$$

  相似的套路，增加m 个球分给每个盒子，分好后从每个盒子中取出一个

第一类斯特林数

补充一下第一类斯特林数

定义
用n 个不同元素构成m 个圆排列的方案数

递推公式

$$S_{n}^{k}=\left ( n-1 \right )*S_{n-1}^{k}+S_{n-1}^{k-1}$$

对于第n 个球
它可以放入前面k 个圆排列中，共有n-1 个不同的位置，也可以自己放入一个新的盒子中

错位排列

定义
每个数都不在自己位置上的方案数

由于通项公式计算计算比较烦琐，且不易取模，这里仅讨论递推公式
递推公式

$$D_{i}=\left ( i-1 \right )\left ( D_{i-1}+D_{i-2} \right )$$

将新加入的元素与每个$D_{i-1}$中的每个元素交换，可生成$\left ( i-1 \right )*D_{i-1}$个合法排列
这样少考虑了一种情况
例如，元素1 在自己位置，元素2-（i-1） 均不在自己位置，这时1 与i 进行交换也可生成合法排列
每个元素均有可能在自己的位置，因此共有$\left ( i-1 \right )*D_{i-2}$种方案
我是在一节语文课上才想通的

重复排列

有k 个元素，每个元素出现$c_{i}$次，$n=\sum c_{i}$
易得方案数

$$\frac{n!}{\prod_{i=1}^{k} c_{i}!}$$

重复组合

有k 个不同的元素，每种元素选择的个数没有限制，选出n 个
问题等价于选n 次，每次可以选k 种球，且不分先后
等价于将n 次选择机会分给k 种球，机会相同，球不同
等价于将n 个相同的球放入k 个不同的盒子，且可以为空
方案数为

$$C_{n+k-1}^{k-1}$$

Catlan数

定义有多种，这里讲其中一种
借用一下神犇wuyiqi 的图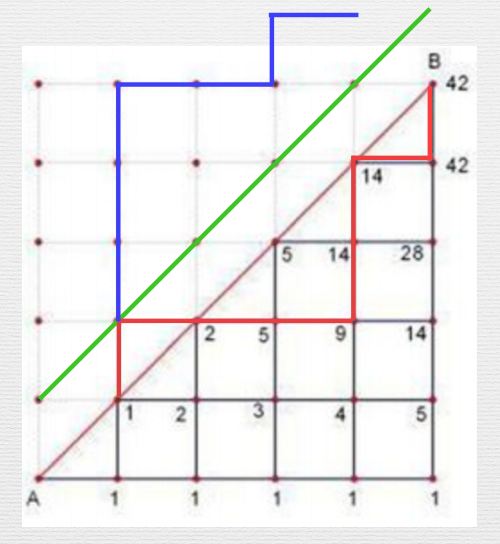

从左下角到右上角，且不穿过对角线的方案数就是Catlan数

任何一种非法方案均与绿线有交点，例如红线
将其按绿线做对称，例如红线与蓝线

可以发现

• 终点均为$\left ( n-1,n+1 \right )$
• 每一种非法方案对应一种$\left ( 0,0 \right )$到$\left ( n-1,n+1 \right )$的方案

所以总方案数为

$$C_{2n}^{n}-C_{2n}^{n-1}=\frac{C_{2n}^{n}}{n+1}$$

再补充两个Catlan数的递推公式

$$T_{n+1}=\frac{4n+2}{n+2}T_{n}$$ $$T_{n+1}=\sum _{i=0}^{n}T_{i}T_{n-i}$$

另外，在上述模型中比较容易求出一个合法前缀$\left ( x,y \right )$的方案数

$$C_{2n-x-y}^{n-x}-C_{2n-x-y}^{n-1-x}$$

先写这一些，其它的等熟练了再补充(･ω´･ )