如果贪心是一只兔子不断往目标跳去,那模拟退火就是一只喝醉的兔子不停乱跳
SA 算法的基本思想是用马尔可夫链的形式进行随机搜索,它不仅接受改善目标函数的变化,而且还能保留一些不理想的变化。
对于改善目标函数的变化直接转移
对于不理想的变化,发生转移的概率为
其中为当前温度,为玻尔兹曼常数,为了方便计算可设
需要设定的参数为初温,末温,和降温系数
适当的温度至关重要
若过大,几乎所有转移都会被接受
若过小,几乎所有不理想的转移均无法被接受,算法将会变为贪心,容易陷入局部最优解
此外,优秀的状态产生函数和状态评估函数将会提高SA的效率最好是能面向数据编程
放一张Wiki的动图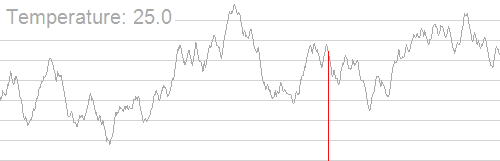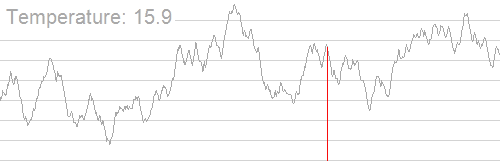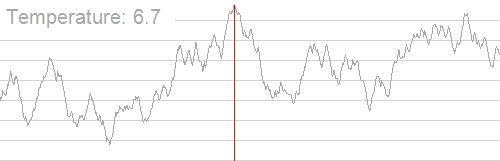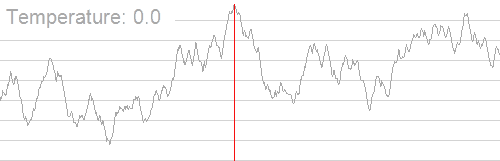
有了SA这题就好写了
状态生产函数采用随机交换两个元素
状态评估函数采用动态规划
设为前i 个分成j 组的最小
调参调了很久1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
using namespace std;
const int N=25,INF=1<<30;
const double st=1e8,ed=1e-5;
const double dt=0.998;
double ave,ans=INF,dp[N][N],s[N];
int n,m,w[N];
inline int read()
{
register int x=0,t=1;
register char ch=getchar();
while (ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
if (ch=='-') t=-1,ch=getchar();
while (ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
return x*t;
}
double pow(double x){return x*x;}
double calc()
{
for(int i=0;i<=n;i++)
for(int j=0;j<=m;j++) dp[i][j]=INF;
for(int i=1;i<=n;i++) s[i]=s[i-1]+w[i];
for(int i=0;i<=m;i++) dp[0][i]=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=min(i,m);j++)
for(int k=j-1;k<=i;k++)
dp[i][j]=min(dp[i][j],dp[k][j-1]+pow(s[i]-s[k]-ave));
return dp[n][m];
}
bool check(double u,double v,double t)
{
return u>v||exp((u-v)/t)*rand()>rand();
}
void SA(double s,double t)
{
double now=calc();
ans=min(ans,now);
while (s>t)
{
int u=rand()%n+1;
int v=rand()%n+1;
if (u==v) continue;
swap(w[u],w[v]);
double nxt=calc();
ans=min(ans,nxt),s*=dt;
if (!check(now,nxt,s))
swap(w[u],w[v]);
else now=nxt;
}
}
int main()
{
srand((unsigned)time(0));
n=read(),m=read();
for(int i=1;i<=n;i++) ave+=w[i]=read();
ave/=m;
SA(st,ed);
printf("%.2lf\n",sqrt(ans/m));
return 0;
}