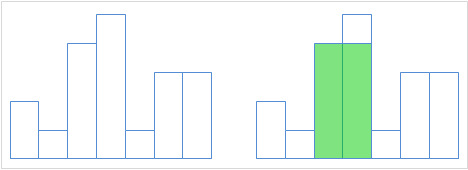
经典题目
这里简要的总结一下它的四种做法最大子矩阵有四种做法,你知道吗
- 单调栈
维护一个单调递增的栈
栈中保存一个二元组,分别为高度和能覆盖到的宽度
一个元素只会在超过它能覆盖的最大宽度后退栈
此时更新答案即可
- 笛卡尔树
笛卡尔树的定义这里就不赘述了
如果有一棵以高度为权值构造好的笛卡尔树
只需一遍dfs 即可得出答案
用单调栈可在时间内建树
维护一个单调递增的栈
对于新加入的元素x ,将最后一个退栈元素作为其左儿子,将其作为栈中top 元素的右儿子
- 并查集
一种看似暴力的做法
实际上复杂度应该是
具体看代码实现
其中L 为当前位置向左能延伸的最大位置,R 为向右的
- 倍增
对于一个区间
找到其最小值所在位置
可将其分为左右两个区间递归处理,且互不影响
倍增数组维护最小值和最小值位置即可
倍增代码就不放了
代码依次给出1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
using namespace std;
struct node {int val,sz;};
int n,x;
LL ans=0;
stack<node> S;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
int sz=0;
ans=max(ans,(LL)x*sz);
while (!S.empty()&&x<=S.top().val)
{
sz+=S.top().sz;
ans=max(ans,(LL)S.top().val*sz);
S.pop();
}
S.push((node){x,sz+1});
}
int sz=0;
while (!S.empty())
{
sz+=S.top().sz;
ans=max(ans,(LL)S.top().val*sz);
S.pop();
}
printf("%lld",ans);
return 0;
}
1 |
|
1 |
|