题目大意：
现有一种过滤器，可以屏蔽以该过滤器为前缀的网站
给出一些需要被屏蔽和不能被屏蔽的网站
无法满足条件输出$-1$
在满足条件的情况下，最小化过滤器的串长之和
按字典序输出所有过滤器

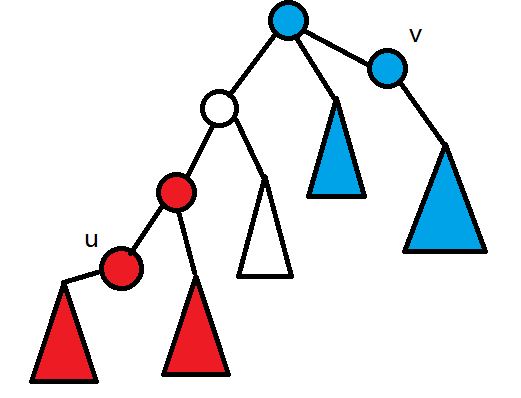
以所有不能被屏蔽网站的名字建立一棵$Trie$
考虑插入每个需要被屏蔽网站的名字的过程

• 若经过的所有节点均是不能被屏蔽的，则无解
• 否则，将开头到第一个未在$Trie$中出现的字符作为一个过滤器，标记该过滤器并退出插入过程
• 若发现当前名字以一个过滤器为前缀，则不需要新增过滤器，可直接退出插入过程

该贪心的正确性显然

题目大意：
给出一个n 个元素的序列，初始值均为0
有两种操作

• 将$\left [ l,r \right ]$的元素+1
• 执行$\left [ l,r \right ]$的所有操作，保证$r$小于当前操作编号

问执行完所有操作后序列中每个元素的值

直接按照操作给出顺序执行会产生递归，无法有效处理
考虑倒着执行操作，这样就没有递归问题了
用一个支持单点查询，区间修改的数据结构维护每个操作执行次数就好了
由于只在操作完询问一次序列中的值
因此序列中的操作用差分即可

本来换行写的是$puts$，不知道为什么$RE$掉了

带修改的莫队
复杂度$O\left ( \sqrt[3]{n^{4}t} \right )$

这题是一道结论题

首先引入$Prufer$序列
定义
$Prufer$序列是一种无根树的编码表示，对于一棵$n$个节点带编号的无根树，对应唯一长度为$n-2$的$Prufer$编码。

转化过程

• 树转$Prufer$序列

  每次找到最小的叶子节点并删除，然后在序列中添加其相邻节点的编号，直至剩下两个节点
  如下图
  
  其$Prufer$序列为$3,5,1,3$
  转化过程用优先队列维护可以做到$O\left ( NlogN \right )$

• $Prufer$序列转树

  设点集$V=\left \{x\mid x\notin Prufer \right \}$
  每次取出$Prufer$序列的$front$，将其与$V$中最小元素连边，并删除这两个元素
  若$front$在之后序列中没有出现，则将其加入$V$
  遍历完整个序列后，将$V$中剩下的两个元素连边
  同样可以用优先队列做到$O\left ( NlogN \right )$

性质与结论

1. 观察上述过程，不难得出$Prufer$序列与树一一对应
   因此可以快速得出一张$n$个点的完全图有$n^{n-2}$棵生成树，即$Cayley$公式

2. 另外，不难发现$Prufer$序列中$x$的出现次数等于$d_{x}-1$，其中$d_{x}$为$x$的度数
   因此当$n$个点的度数分别为$d_{1},d_{2}\dots d_{n}$时，共有$\frac{\left(n-2\right)!}{\prod \left ( d_{i}-1 \right )!}$种生成树

3. 更一般的，当其中$x$个点度数已知，$y$个点度数未知时
   记

   $$sum=\sum_{i=1}^{x}\left ( d_{i} -1\right )$$

   首先考虑$x$个已知节点的方案
   不难得出

   $$C_{n-2}^{sum}*\frac{sum!}{\prod_{i=1}^{x}\left ( d_{i}-1 \right )!}$$

   然后是$y​$个未知节点
   考虑到每个未填位置均有$y$种可能，共有$y^{n-2-sum}$种方案
   根据乘法原理，总方案数为

   $$C_{n-2}^{sum}*\frac{sum!}{\prod_{i=1}^{x}\left ( d_{i}-1 \right )!}*y^{n-2-sum}$$

代码就不放了

题目大意：
求

$$\left ( \sum_{i=1}^{n}i^{4}\left \lfloor \frac{n}{i} \right \rfloor \right )\% M$$

套路是很常见的分块求解
难点主要是$i^{4}$求和，$M$不一定为质数

首先有如下几个恒等式

$$\sum_{i=1}^{n}i^{2}=\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}$$ $$\sum_{i=1}^{n}i^{3}=\left ( \frac{n\left ( n+1 \right )}{2} \right )^{2}$$ $$\sum_{i=1}^{n}i^{4}=\frac{n\left ( n+1 \right )\left ( 2n+1 \right )\left ( 3n^{2} +3n-1\right )}{30}$$

其中平方和公式推导如下
$\left ( n+1 \right )^{3}-n^{3}=3n^{2}+3n+1$
$n^{3}-\left ( n-1 \right )^{3}=3\left ( n-1 \right )^{2}+3\left ( n-1 \right )+1$
$\cdots$
累加得

$$\left ( n+1 \right )^{3}-1^{3}=3*\sum_{i=1}^{n}i^{2}+3*\sum_{i=1}^{n}+n$$

化简可得

$$\sum_{i=1}^{n}i^{2}=\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}$$

立方和，四次方和同理可得

然后是$M$不为质数的问题
有如下公式

$$\frac{a}{b}\%c=\frac{a\%\left (bc \right )}{b}$$

然而我以前一直都不知道

三色**

首先考虑两种颜色，分别在u，v
由于路径唯一，两种颜色还是比较好求的
只要取$\left ( u,v \right )$路径中点，将树分为两半即可，每个点分别控制一半
如图

现在有三种颜色，也就是求交集
求交集可以用线段树，先把树转化为dfs 序，然后第一次区间加，第二次区间询问

不知道为什么写挂了，于是写了个分类讨论
记录一个二元组$\left ( opt,x \right )$，$x$为子树根节点，$opt=1$表示可选，0 则表示不可选
观察到两棵子树之间只有两种关系，要么不相交，要么一棵树是另一棵树的子树
判断是否相交用$LCA$即可
然后分类讨论，设两棵子树分别以$A$，$B$为根，且$A_{sz}\leq B_{sz}$

• 均可选，若两棵子树不相交则为0 ，否则为$A_{sz}$
• 均不可选，若两棵子树不相交则为$n-A_{sz}-B_{sz}$，否则为$B_{sz}$

• 一个可选，一个不可选

  设$A_{opt}=1$，$B_{opt}=0$，这里对$sz$没有要求

  • $LCA\left ( A,B \right )=A$，答案为$A_{sz}-B_{sz}$
  • $LCA\left ( A,B \right )=B$，答案为0 ，但事实上并不会出现这种情况
  • 否则为$A_{sz}$

乍一看以为裸的树剖
后来发现事情没那么简单，$c_{k}-c_{j}$是有顺序的，$j\leq k$

第一问很简单
第二问维护一大堆倍增数组

首先$fa$不用说，然后是$mx$，$mn$记录往上走的最大（最小）值
还需要$f$记录上面节点-下面节点的最大值，$g$记录下面节点-上面节点的最大值

预处理

$$mx\left [ x \right ]\left [ i \right ]=max\left ( mx\left [ x \right ]\left [ i-1 \right ] ,mx\left [fa\left [ x\right ] \left [ i-1 \right ]\right ]\left [ i-1 \right ]\right )$$ $$mn\left [ x \right ]\left [ i \right ]=min\left ( mn\left [ x \right ]\left [ i-1 \right ] ,mn\left [fa\left [ x\right ] \left [ i-1 \right ]\right ]\left [ i-1 \right ]\right )$$ $$f\left [ x \right ]\left [ i \right ]=max\left ( f\left [ x \right ]\left [ i-1 \right ] ,f\left [fa\left [ x\right ] \left [ i-1 \right ]\right ]\left [ i-1 \right ],mx\left [ fa\left [ x\right ] \left [ i-1 \right ] \right ]\left [ i-1 \right ]-mn\left [ x \right ]\left [ i-1 \right ]\right )$$ $$g\left [ x \right ]\left [ i \right ]=max\left ( g\left [ x \right ]\left [ i-1 \right ] ,g\left [fa\left [ x\right ] \left [ i-1 \right ]\right ]\left [ i-1 \right ],mx\left [ x \right ]\left [ i-1 \right ]-mn\left [ fa\left [ x\right ] \left [ i-1 \right ] \right ]\left [ i-1 \right ]\right )$$

有了这些倍增数组之后就好求解了
记$LCA\left ( u,v \right )$为$pre$，将$\left ( u,v \right )$拆为$\left ( u,pre \right )$，$\left ( pre,v \right )$两条链
首先$max\left ( pre,v \right )-min\left ( u,pre\right )$肯定合法

然后考虑怎么求$\left ( u,pre \right )$的答案
设在倍增时已跳到$x$，用一个$num$记录$\left ( u,x \right )$的最小值
则下一次跳跃时

$$ans=max\left \{ f\left [ x \right ] \left [ i \right ],mx\left [ x \right ]\left [ i \right ]-num\right \}$$

之后更新$num$

$$num=min\left \{ mn\left [ x \right ]\left [ i \right ] \right \}$$

同理可求$\left ( pre,v \right )$的答案，用$num$记录最大值即可

如果问题是在一个区间上的，那就成了一个经典的贪心问题
将所有区间按照右端点升序排序之后，每个未满足的区间尽可能向右染即可

在树上也可以贪心
将所有链按父节点深度降序排序之后，每条未满足的链尽可能往高处染

• 因为是按照父节点深度降序，如下图，在处理红链时不可能出现未处理的蓝链
  
• 对于每条未满足的链，显然染的越高能覆盖的就越多

题目大意：
给出一棵以1 为根的树
Alice在1，Bob在x
两人轮流操作，Bob先走
当两人相遇时游戏结束
Bob希望相遇越晚越好，Alice希望相遇越早越好
问游戏最多能进行几轮

观察到Bob一定在Alice的子树内
因此Alice不停向Bob移动即可

Bob则有两种选择

• 在当前点往深度最深的点走
• 先往上走几步，再往深度最深的点走

考虑枚举终点y，记pre 为$LCA\left ( x,y \right )$
当且仅当$dep\left [ pre \right ]-dep\left [ rt \right ]>dep\left [ x \right ]-dep\left [ pre \right ]$，Bob可以走到y
且终点在y 时，最多能进行$2*\left ( dep\left [ y \right ]-dep\left [ rt \right ] \right )$轮

题目大意：
给出一棵n 个节点树
去掉其中一条边，再重新加入一条长度相同的边
问新树中任意两点之间距离的总和最小是多少

原树去掉一条边之后变为两棵树，分别记为A，B，它们的节点个数分别为$A_{sz}$，$B_{sz}$
设去掉边长度为d，新连接的两点分别为u，v
记A 中所有点到u 距离之和为$S_{u}$，同理$S_{v}$
记A 中任意两点的距离之和为$C_{A}$，同理$C_{B}$

新树中任意两点的距离和分两部分考虑

• 在A，B 树内，即$C_{A}+C_{B}$

• 在两棵树之间

  例如$x-u-v-y$，其中x 为A 中的节点，y 为B 中的节点
  将这样的路径分三部分考虑

  • 首先是$u-v$，不难发现共经过$A_{sz}*B_{sz}$次
  • 然后是$x-u$，每个$x-u$都会经过$B_{sz}$次
  • 同理$v-y$

全部加起来就是

$$C_{A}+C_{B}+d*A_{sz}*B_{sz}+S_{u}*B_{sz}+S_{v}*A_{sz}$$

观察到$C_{A},C_{B},d,A_{sz},B_{sz}$与$u,v$无关
因此只需找$S_{u},S_{v}$最小的$u,v$

关于$S$的计算分为两个部分，以A 树为例

• 第一遍dfs 求出每个节点x 的子树大小和子树中节点到x 的距离和

  $$S_{x}+=S_{x_{son}}+val_{x-x_{son}}*sz_{x_{son}}$$

• 第二遍dfs

  $$S_{x_{son}}=S_{x}+val_{x-x_{son}}*\left (A_{sz}-sz_{x_{son}} \right )-val_{x-x_{son}}*sz_{x_{son}}$$

  ​ 就是把中心点从x 移到$x_{son}$，$\left (A_{sz}-sz_{x_{son}} \right )$多经过一条边，$sz_{x_{son}}$少经过一条边

有了$S$，$C$就好计算了

$$C_{A}=\frac{\sum _{x \in A} S_{x}}{2}$$

每条边$x-y$，会在x，y 各计算一次